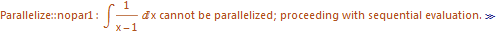Как сделать команды в Mathematica 8 использовать все ядра?

Как упоминалось в других вопросах и комментариях, такие вещи, как Integrate и Simplify было бы очень трудно распараллелить, поэтому Mathematica возвращает сообщение Parallelize::nopar1 и продолжает " с последовательной оценкой."

(хотя по размышлению, может быть FullSimplify можно распараллелить, так как это в принципе строительство, пробуя множество различных правил и делать leafcounts на них...)

если у вас много интегралов или упрощений, то вы можете использовать ParallelTable или ParallelMap etc...

банальный пример, если у вас есть подынтегральные

In[1]:= ints = Table[x^n, {n, 1, 10}]
Out[1]= {x, x^2, x^3, x^4, x^5, x^6, x^7, x^8, x^9, x^10}

можно использовать ParallelTable

In[2]:= ParallelTable[Integrate[int, x], {int, ints}]
Out[2]= {x^2/2, x^3/3, x^4/4, x^5/5, x^6/6, x^7/7, x^8/8,\ 
         x^9/9, x^10/10, x^11/11}

или ParallelMap

In[3]:= ParallelMap[Integrate[#, x] &, ints]
Out[3]= {x^2/2, x^3/3, x^4/4, x^5/5, x^6/6, x^7/7, x^8/8,\  
         x^9/9, x^10/10, x^11/11}

очевидно, что для небольших списков интегралов, подобных приведенному выше, издержки распараллеливания, вероятно, больше, чем выгода. Но если у вас действительно большие списки и сложные интегралы, то это, вероятно, стоит того.

редактировать в ответ на комментарии

учитывая действительно грязный подынтегральную, что ОП заинтересован в (Примечание: Вы должны действительно упростить свои результаты, как вы идете!), вот некоторый код, который разбивает Интеграл на сумму мономов и выполняет интегралы, используя ParallelDo.

сначала импортируем Интеграл из pastebin

In[1]:= import = Import["http://pastebin.com/raw.php?i=JZ0CXewJ", "Text"];

извлечь домен интеграции

In[2]:= intLimits = Rest@(2 Pi^5 ToExpression[StringReplace[import, "Integrate" -> "List"]])
        vars = intLimits[[All, 1]];

Out[2]= {{\[Theta]3, 0, 2*Pi}, {\[Theta]2, 0, 2*Pi}, 
         {\[Theta]1, 0, 2*Pi}, {\[CurlyPhi]2, 0, Pi/2}, {\[CurlyPhi]1, 0, Pi/2}}

и подынтегральная функция, которая приходит как сумма 21 чудовищного условия

In[4]:= integrand = First@(2 Pi^5 ToExpression[StringReplace[import, "Integrate" -> "Hold"]]);
        Length[integrand]
        LeafCount[integrand]

Out[5]= 21
Out[6]= 48111

нам нужно разбить ужасный беспорядок на кусочки размером с укус. Сначала мы извлекаем все различные функции из интеграла

In[7]:= (fns=Union[vars, Cases[integrand, (Cos|Sin|Tan|Sec|Csc|Cot)[x_]/;!FreeQ[x,Alternatives@@vars],Infinity]])//Timing
Out[7]= {0.1,{\[Theta]1, <snip> ,Tan[\[CurlyPhi]2]}}

мы находим (13849 ненулевых) коэффициенты мономов, построенных из fns

In[8]:= coef = CoefficientRules[integrand, fns]; // Timing
         Length@coef

Out[8]= {35.63, Null}
Out[9]= 13849

убедитесь, что все коэффициенты не содержат интегральных переменных

In[10]:= FreeQ[coef[[All, 2]], Alternatives@@vars]
Out[10]= True

обратите внимание, что мы можем очистить коэффициенты, используя Factor или Simplify и уменьшить ByteSize примерно в 5 раз... Но поскольку интегралы большинства мономов равны нулю, мы могли бы также оставить упрощения до самого конца.

это, как вы восстановить одночлены, интегрировать его и рекомбинируют с ее коэффициент, например, 40-й МОНом дает неувядающий Интеграл:

In[11]:= monomialNum=40;
         Times@@(fns^coef[[monomialNum,1]])
         Integrate[%, Sequence@@intLimits]
         coef[[monomialNum,2]] %//Factor
Out[12]= \[Theta]1 Cos[\[Theta]1]^2 Cos[\[CurlyPhi]1]^4 Cos[4 \[CurlyPhi]1] Cos[\[CurlyPhi]2]^4 Cos[2 \[CurlyPhi]2] Sin[\[Theta]1]^2
Out[13]= \[Pi]^6/256
Out[14]= -((k1^2 (k1-k2) (k1+k2) (-2+p) p^3 \[Pi]^6 \[Sigma]^4)/(131072 \[Omega]1))

на данный момент я уменьшу количество терминов, так как потребуется вечность, чтобы сделать все интегралы на моем двухъядерном ноутбуке. Удалить или комментарий из следующей строки, Когда вы хотите оценить весь набор интегралов

In[15]:= coef = RandomChoice[coef, 100];  (* Delete me!! *)

OK, инициализировать пустой список результатов мономиальной интеграции

In[16]:= SetSharedVariable[ints]
         ints = ConstantArray[Null, Length@coef];

как мы выполняем интегралы, мы Print out num: {время, результат} для каждого мономиального интегрированного. The CellLabel каждой напечатанной клетки говорит вам, какое ядро сделал Интеграл. Печать может раздражать-если она вас раздражает, затем замените Print С PrintTempory или ##&. Вы также можете отслеживать вычисления, используя какую-либо динамическую переменную: например, a прогресс-бар.

ParallelDo[Print[c, ": ", Timing[
            ints[[c]] = Integrate[Times@@(fns^coef[[c,1]]), Sequence@@intLimits]]], 
           {c, Length@coef}]

объединить с их коэффициентами

1/(2 Pi^5) Simplify[ints.coef[[All, 2]]]

и (надеюсь) вот так!